When we returned from winter break, our Algebra learners hit the road running and began our unit over polynomials. As I told both classes, this is one of my favorite units and to be prepared for an over excited teacher! This of course brought smiles to their faces and reignited their passion for growing in their mathematical knowledge.
To kick off our unit, learners focused on naming polynomials as well as adding and subtracting polynomials. Much to their surprise, they already had experiences with both concepts! The relief was much needed after learning about exponents and radicals, where their brains were stretched and thinking outside of the box occurred on a daily basis.
We focused on finding the area and perimeter of various figures, which would serve as a foundation as we began to multiply and divide polynomials. To kick off learning about multiplying polynomials, I had learners text their parents asking if they remembered using FOIL in math.
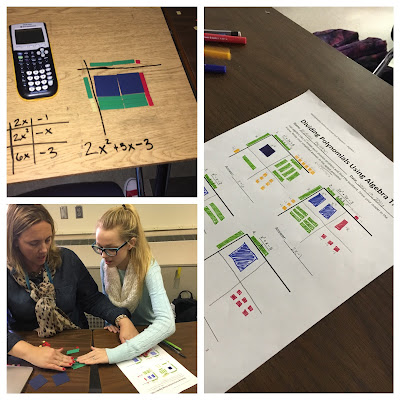
As the dings of arriving text messages filled the air and learners were excited to share their parents' responses, we pulled out the algebra tiles and began to multiply polynomials! From the sounds in our classroom, plus the need to use our fancy colored pens, learners were excited to create. Little did they realize their creations were creating concrete examples for their minds to use to make connects to an abstract concept!
As we continued to build our models with algebra tiles, we connected our "playing" with the box method. Learners were amazed at how easy they were able to explain how to find the product of polynomials by using either method. To stretch their thinking I gave various representations of the same problem and had learners recreate the other representations.
 |
| Given 1 representation & asked to create the others |
I'm quite impressed with the learners of room 27 this week, as they embraced being a kid again and playing in math! Too many times we get caught up in being an advanced academic student, rather than embracing a growth mindset. This week was one that was filled with critical thinking, problem solving and most of all successful learners!

Based on the success of these learning opportunities, we began division on Friday! Thinking was challenged and connections were made. One learner was overhead saying, "This is hard. My brain can't understand this." I was quick to remind him that we were all going to stretch our thinking and learn about dividing polynomials in a method other than an algorithm.
Pages began to be flipped, algebra tiles began to spill on the desks and boxes began to be drawn on the desk. Thinking backwards from what they knew about multiplying polynomials allowed learners to create their own solutions for dividing polynomials.
As part of their assessment over polynomials, learners will be asked to write a letter to a 5th grader explaining how to use concrete examples to explain how to solve problems with polynomials.








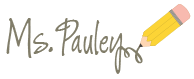
No comments